Naučna pismenost, slično kao i bilo koja druga varijanta pismenosti, podrazumeva uspešno pisanje i čitanje, odnosno slanje i primanje poruka koje sadrže naučno relevantne informacije. Onaj ko šalje poruku je, uglavnom, onaj ko o konkretnoj temi zna najviše, tj. onaj ko neposredno istražuje problem i vidi sve detalje. Taj neko je istraživač u najširem smislu reči. Slično kao i u vreme Marka Pola i otkrivanja novih teritorija, istraživači idu pre ostalih, vide razne stvari i proživljavaju mnogo toga da bi potom sumirali svoja iskustva, saznanja i utiske i konačno ih predali svoj publici u formi priče, putopisa ili nekakve mape. Istraživači nikada ne mogu da prenesu celokupno svoje iskustvo, niti za to ima potrebe. Istraživačko iskustvo mora da se profiltrira i sažme u određenu formu koja će ukazati na sve što je bitno, ali ne više od toga. Jedan od najefektnijih načina prenošenja naučnih informacija je grafički prikaz ili dijagram.

ako znamo da ih koristimo,
dijagrami predstavljaju
moćne alatke

On podrazumeva vremenske serije, skice predmeta, geografske karte itd., odnosno sve ono gde reči više nisu dovoljno efikasne, tj. gde puno toga hoćemo da stavimo na malo papira. Poznata fraza da slika vredi kao hiljadu reči zapravo je prilično dobra procena vrednosti tipične slike u naučnim radovima. Međutim, ne vredi uvek toliko. Upravo o tome hoću da vam kažem neku reč.
Najveći broj dijagrama crtamo sami sebi zato što nam je često potreban još jedan način da predstavimo empirijske podatke. Grafičko prikazivanja podataka može da ponudi mnogo više od slikovne zamene za tabele podataka. Ako znamo da ih koristimo, dijagrami postaju moćne alatke za zaključivanje o kvantitativnim informacijama. Često, najefektivniji način za opisivanje, ispitivanje i sumiranje skupa brojeva je da posmatramo sliku koja te brojeve predstavlja. Dijagrami, takođe, služe i kao podsetnik. Neke ideje nije lako artikulisati u reči. Lakše je napraviti skicu. Svega nekoliko linija može da nam pomogne da rekonstruišemo ceo misaoni tok. To je rečima mnogo teže učiniti. Zbog toga istraživači dok istraživanje još traje stalno crtaju grafike, histograme raspodela, konceptualne mape itd.
Kada informacije prenosimo nekom drugom, dobro dizajniran dijagram je najjednostavniji i najbolji način da to uradimo. Zamislite koliko bi reči trebalo da se opiše kako sklopiti igračku iz kinder-jajeta; umesto toga, gruba skica sa nekoliko brojeva i strelica odlično rešava problem. Komunikacija istraživača samog sa sobom, jasno, ne mora da pati od konvencionalnih ograničenja. Međutim, kada slikovnu poruku šaljemo nekom drugom, situacija je bitno drugačija. Najinteresantnija ciljna grupa su krajnji korisnici, tj. oni koji rezultate ne koriste za dalja istraživanja već samo za donošenje odluke, npr. da li da kupe neki proizvod, da li da odobre sredstva za finansiranje nekog projekta ili da li da proglase epidemiju. Ne postoji idealan način grafičkog predstavljanja rezultata. Na koji način bi bilo najbolje da predstavimo rezultate zavisi, pre svega, od toga šta o pojavi koja je opisana dijagramom korisnici znaju. Čuveni statističar iz prethodnog veka, Džon Tuki je rekao da grafik dostiže punu vrednost kad nas primora da vidimo ono što je neočekivano. Ovaj iskaz ima veliku praktičnu vrednost. Da bismo optimalno prikazali podatke, treba da utvrdimo šta je za korisnika neočekivano, tj. koliko zna o pojavi sa grafika. Korisniku uvek možemo da olakšamo posao tako što mu damo mogućnost da podatke uporedi sa nečim poznatim ili očekivanim po određenoj logici ili modelu. Ipak, uspešnost grafičkog predstavljanja podataka zavisi najviše od naše procene kako će to korisnik protumačiti.
Činjenica da su krajnji korisnici dijagrama uvek donosioci odluka, celu stvar sa crtanjem i čitanjem dijagrama čini ozbiljnijom. Ako pogledate neki izveštaj sa podnaslovom „executive summary“ sigurno ćete videti dijagrame koji bi trebalo da pomognu u došenju odluka. Nažalost, ti dijagrami su prečesto šarene "pitice" koje zapravo nose minimum informacija predstavljenih u vrlo nepreglednoj formi. Razlog za ovo mogu da budu dve stvari: ili autori ne znaju da naprave dijagram koji ističe ono što je bitno ili donosioci odluka ne znaju da pročitaju dijagram koji je složeniji od sektorskih dijagrama. Posledice loše komunikacije ovog tipa mogu da budu katastrofalne. Najpoznatiji primer je eksplozija spejs-šatla Čelendžer 28. januara 1986. zbog toga što su neki O-prstenovi procureli usled niske spoljne temperature. Tada je na očigled stotina miliona televizijskih gledalaca stradalo svih sedam članova posade. Ono što je tad zakazalo nisu bili inženjeri. Oni su odmah reagovali čim su čuli vremensku prognozu i rekli da bi let trebalo odložiti. Međutim način na koji su svoje argumente predstavili (13 dijagrama iz kojih je teško videti celinu) nije bio dovoljno ubedljiv. Sve je to

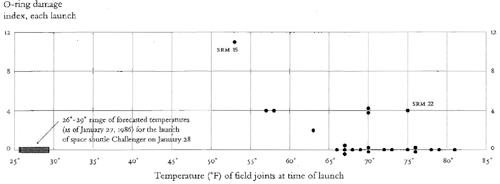
moglo da se stavi na jedan grafik koji ne bi ostavio mnogo dileme da li odobriti let ili ne. Pogledajte grafikon na prethodnoj strani i uverićete se koliko je jednostavan i kobno predvidljiv. Let je, međutim, odobren i tragedija je bila neizbežna.

Prema Edvardu Taftiju izuzetnost u grafičkom
prikazivanju rezultata sastoji se od jasnog, preciznog
i efikasnog prenošenja kompleksnih
ideja. Ukratko, on kaže da dijagrami treba da:
- prikažu podatke
- navedu posmatrača da razmišlja o suštini
pre nego o grafičkom dizajnu i tehnici kojom
je dijagram proizveden itd.
- izbegnu mogućnost da prikaz iskrivi ono što
o podacima treba reći
- predstave puno brojeva na malom prostoru
- velike skupove podatka učine koherentnim
- ohrabre posmatrača da poredi različite delove
skupa podataka
- otkriju podatke na više nivoa detaljnosti, od
opšteg pregleda do fine strukture
- služe jasno određenoj svrsi: opisivanju, istraživanju,
klasifikovanju ili dekoraciji
- budu čvrsto integrisani sa statističkim i verbalnim
opisima skupa podataka.

Problem je nesumnjivo u tome što većina ljudi crtanje grafika i drugih dijagrama doživljava kao potpuno tehničku stvar. To je zapravo isto kao da tehničkom stvari smatraju pisanje teksta, tj. da tekst zavisi od toga da li koristimo Word ili Open Office. Jednom rečju – zabrinjavajuće. Istina je da nam raznovrsni softverski alati za crtanje grafika drastično olakšavaju posao, ali nam sigurno neće reći šta je to od podataka bitno a šta ne i, što je još važnije, nikako nas ne oslobađaju odgovornosti za to što radimo. Računar će naše podatke pretvoriti u dijagram tačno onako kako mu to mi kažemo. Da bismo znali šta da mu kažemo, potrebno je dijagrame vratiti u školu. Kad smo počeli da učimo o brojevima crtali dijagrame sa pet kružića ili sedam jabuka. Tablić smo igrali, verovatno još pre škole, i „lupali recke“ ne znajući da je i to dijagram. Posle toga, nažalost, dijagrami su polako iščezli. Na međunarodnom TIMSS istraživanju za osmake, gde se ispituje ono što je u programima većine zemalja koje na ispitivanju učestvuju, naši đaci se redovno sreću sa nepoznatom rečju histogram. (Nije ni čudo, evo sad mi i ovaj srpski spell-checker reč histogram podvlači crveno!) Izgleda da većina zemalja smatra da je korišćenje i razu-mevanje histograma neophodno svim građanima. Kod nas to, očigledno, nije slučaj. Kod nas je čak i crtanje grafika u smislu predstavljanje uređenih parova u pravouglom koordinatnom sistemu inkriminisano pre osmog razreda, jer se vezuje za grafike funkcija, koje se, eto, u osmom razredu uče. Da li je neophodno da znamo šta su funkcije da bismo tačku stavili na koordinate x=3 i z=2?
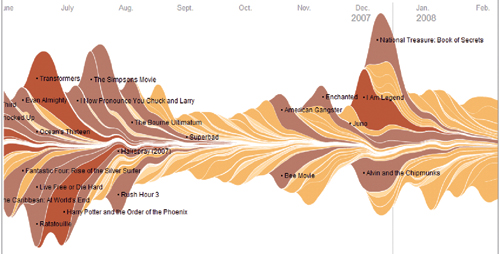
Umesto zaključka, ovde kao primer dajem jedan grafički prikaz iz nekih dnevnih novina koji izlaze daleko odavde. Voleo bih da jednog dana tako nešto vidim i kod nas kad otvorim novine.

KRATAK SPISAK SUGESTIJA ZA DALJE ČITANJE
- How to Lie with Statistics, Darrell Huff, Penguin
Business, 1954
- Visual Display of Quantitative Information, Edward
Tufte, Graphics Press, 1992
- Gallery of Data Visualization – The Best and Worst of
Statistical Graphics, www.math.yorku.ca/SCS/Gallery/
- R Graph Gallery, http://addictedtor.free.fr/graphiques/
- Gapminder, Hans Rosling, http://www.gapminder.org

[sci-literacy]

“SCIENTIFIC (IL)LITERACY” is a section of the “Petnica” almanac where professionals have opportunity to discuss some actual issues related to the science policy, especially the problems of public understanding the science and technology.

graphs are made by people

Drawing of graphs is often treated as purely technical thing. When you collect and analyze all your data, it should be trivial to make the scatter plot or some other diagram. However, drawing of diagrams is much more than that; it is completely new stage in data analysis and definitely not the end of research. Drawing of graphs and observing what you get is powerful analytical tool, not only the way to present your results to your peers. In this article, Srdjan Verbić is putting “graphical writing and reading” in the context of general scientific literacy. Reading of diagrams is already incorporated in competencies required by reading literacy. On the other side, effective drawing and interpretation of scientific diagrams belong to higher levels of scientific literacy.
Visual display of quantitative information (as Edward Tufte named all graphical aids accompanying empirical data) is important for researchers themselves as well as for ultimate users of information, i.e. decision makers. It is likely that important data will appear in some visual form in summary reports addressed to directors, presidents of funds or committees, etc. Therefore, we can expect that those people will decide not on the basis of results but on the basis of impression they get from some pie-chart or some other inadequate visual display.
The well-known sentence made by John Tukey 30 years ago that “the greatest value of a graph is when it forces us to see what we never expected” can have some practical implications. If you know who are you drawing your graph to, try to estimate how much that person knows about the problem described by the graph. If you make a good estimation, you will get close to what that person considers to be “expected” and “unexpected”. Then you will know how to make the most effective diagram.
Finally, author is pointing to contemporary status of diagrams in Serbian education system. Some important concepts concerning graphical tools and graphical presentation of data are omitted from curricula. The obvious consequence is more difficult science communication, especially between scientists and the general public.